
Maximizing l( λ) is quadratic programming (QP) problem, specified by (10). In conclusion, maximizing l( λ) is the main task of SVM method because the optimal weight vector W * is calculated based on the optimal point λ * of dual function l( λ) according to (8). Thus, setting the gradient of L( W, b, ξ, λ, μ) with respect to W, b, and ξ to zero, we have:Īccording to Lagrangian duality problem represented by (7), λ=( λ 1, λ 2,…, λ n) is calculated as the maximum point λ * =( λ 1 *, λ 2 *,…, λ n *) of dual function l( λ). If gradient of L( W, b, ξ, λ, μ) is equal to zero then, L( W, b, ξ, λ, μ) will gets minimum value with note that gradient of a multi-variable function is the vector whose components are first-order partial derivative of such function. Thus, the Lagrangian function L( W, b, ξ, λ, μ) is minimized with respect to the primal variables W, b and maximized with respect to the dual variables λ=( λ 1, λ 2,…, λ n) and μ=( μ 1, μ 2,…, μ n), in turn. Now it is necessary to solve the Lagrangian duality problem represented by (7) to find out W *. Where Lagrangian function L( W, b, ξ, λ, μ) is specified by (6). According to Lagrangian duality theorem, the pair ( W *, b *) is the extreme point of Lagrangian function as follows: The ultimate goal of SVM method is to find out W * and b *. It is easy to infer that the pair ( W *, b *) represents the maximum-margin hyperplane and it is possible to identify ( W *, b *) with the maximum-margin hyperplane. Note that W * is called optimal weight vector and b * is called optimal bias. Suppose ( W *, b *) is solution of constrained optimization problem specified by (5) then, the pair ( W *, b *) is minimum point of target function f( W) or target function f( W) gets minimum at ( W *, b *) with all constraints. The sign " " denotes scalar product and every training data point X i was assigned by a class y i before. Note that λ=( λ 1, λ 2,…, λ n) and μ=( μ 1, μ 2,…, μ n) are called Lagrange multipliers or Karush-Kuhn-Tucker multipliers or dual variables. The Lagrangian function is constructed from constrained optimization problem specified by (5). If the positive penalty is infinity, then, target function f( W) may get maximal when all errors ξ i must be 0, which leads to the perfect separation specified by (4).Įquation (5) specifies the general form of constrained optimization originated from (4). The penalty is added to the target function in order to penalize data points falling into the margin.

We have a n-component error vector ξ=( ξ 1, ξ 2,…, ξ n) for n constraints. On the other hand, the imperfect separation allows some data points to fall into the margin, which means that each constraint function g i( W, b) is subtracted by an error.
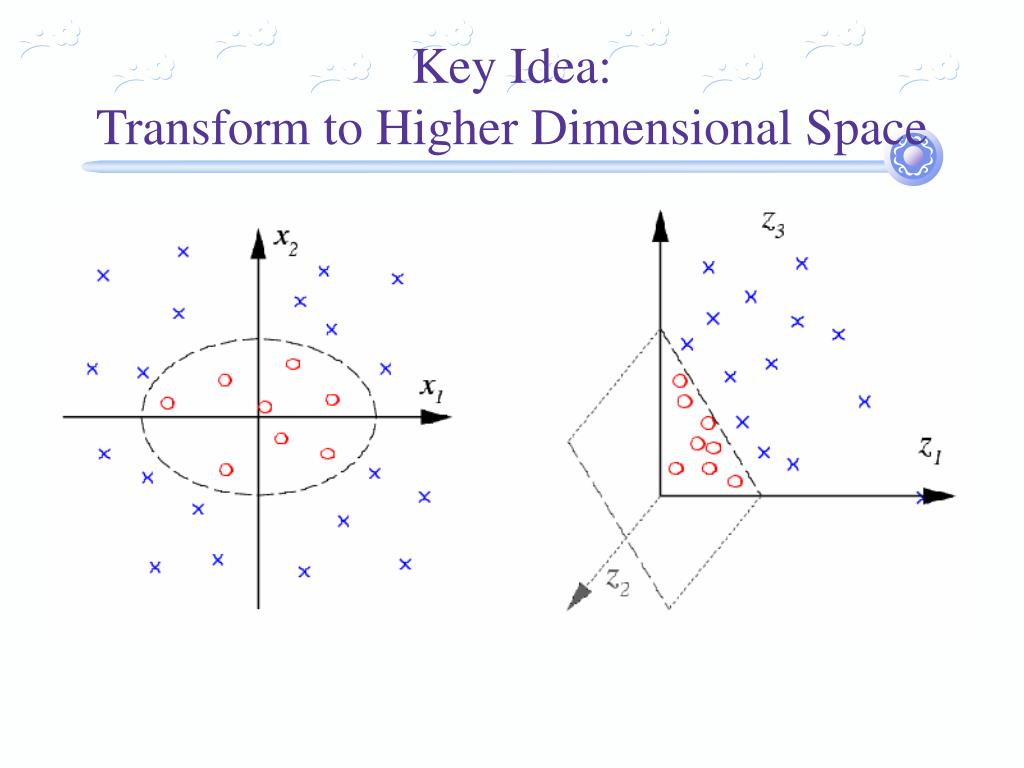
Constraints inside (3) implicate the perfect separation in which there is no data point falling into the margin (between two parallel hyperplanes, see fig. Such hyperplane is called maximum-margin hyperplane and it is considered as the SVM classifier. In other words, the nearest between one side of this hyperplane and other side of this hyperplane is maximized. We can find many p–1 dimensional hyperplanes that classify such vectors but there is only one hyperplane that maximizes the margin between two classes. Suppose we have some p-dimensional vectors each of them belongs to one of two classes. 1 shows separating hyperplanes H 1, H 2, and H 3 in which only H 2 gets maximum margin according to this condition. There is the condition for this separating hyperplane: "it must maximize the margin between two sub-sets". Given a set of p-dimensional vectors in vector space, SVM finds the separating hyperplane that splits vector space into sub-set of vectors each separated sub-set (so-called data set) is assigned by one class. Support vector machine (SVM) is a supervised learning algorithm for classification and regression.


 0 kommentar(er)
0 kommentar(er)
